Levenshtein-Algorithmus

Copyright © Shutterstock/whiteMocca
Was ist der Levenshtein-Algorithmus?
In der Informationstheorie, Linguistik und Informatik ist der Levenshtein-Algorithmus oder die Levenshtein-Distanz eine String-Metrik zur Messung der Differenz zwischen zwei Sequenzen. Informell ist der Levenshtein-Algorithmus zwischen zwei Wörtern die minimale Anzahl von Ein-Zeichen-Bearbeitungen (Einfügungen, Löschungen oder Ersetzungen), die erforderlich sind, um ein Wort in das andere zu ändern. Der Algorithmus ist nach dem sowjetischen Mathematiker Vladimir Levenshtein benannt, der diese Entfernung 1965 in Betracht zog.
Die Grenzen
Der Levenshtein-Algorithmus besitzt mehrere obere und untere Grenzen:
- Es besteht mindestens der Größenunterschied zwischen den beiden Strings.
- Die maximale Länge ist die des längeren Strings.
- Das Ergebnis beträgt nur 0 wenn die beiden Strings gleich sind.
- Wenn die Strings die gleiche Größe haben, ist die Hamming-Distanz eine obere Grenze für die Levenshtein-Distanz.
- Die Levenshtein-Distanz zwischen zwei Strings ist nicht größer als die Summe ihrer Levenshtein-Abstände von einer dritten Strings (Dreiecksungleichung).
Anwendungen
Bei der annähernden Zeichenfolgenübereinstimmung besteht das Ziel darin, Übereinstimmungen für kurze Zeichenfolgen in vielen längeren Texten zu finden, in Situationen, in denen eine kleine Anzahl von Unterschieden zu erwarten ist. Hier ist eine der Strings typischerweise kurz, während die andere beliebig lang ist. Dies hat eine breite Palette von Anwendungen, zum Beispiel Rechtschreibprüfung, Korrektursysteme für die optische Zeichenerkennung und Software zur Unterstützung der Übersetzung natürlicher Sprache basierend auf Translation Memory.
Man kann die Levenshtein-Distanz auch zwischen zwei längeren Strings berechnen, aber die Kosten, um sie zu berechnen, was grob proportional zu dem Produkt der zwei Stringlängen ist, macht dies unpraktisch. Wenn sie verwendet werden, um bei der Suche nach unscharfen Zeichenfolgen in Anwendungen, wie zum Beispiel einer Datensatzverknüpfung, zu helfen, sind die verglichenen Zeichenfolgen normalerweise kurz, um die Geschwindigkeit der Vergleiche zu verbessern.
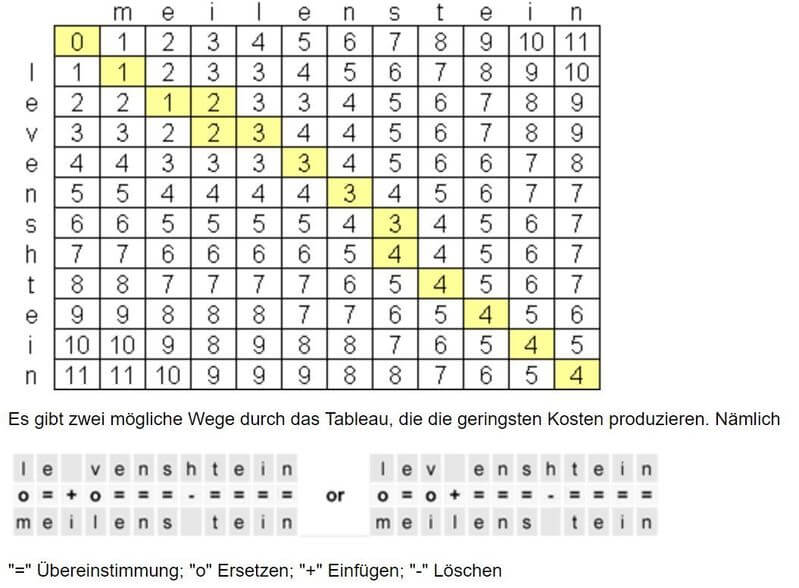
Beispiel zum Levenshtein-Algorithmus / Screenshot levenshtein.de/
Sie haben noch Fragen?